ଡିଜାଇନ୍ଫଟୋନିକ୍ସମନ୍ୱିତ ପରିପଥ
ଫଟୋନିକ୍ ସମନ୍ୱିତ ସର୍କିଟ୍(PIC) ପ୍ରାୟତଃ ଗାଣିତିକ ସ୍କ୍ରିପ୍ଟ ସାହାଯ୍ୟରେ ଡିଜାଇନ୍ କରାଯାଏ କାରଣ ଇଣ୍ଟରଫେରୋମିଟର କିମ୍ବା ପଥ ଦୈର୍ଘ୍ୟ ପ୍ରତି ସମ୍ବେଦନଶୀଳ ଅନ୍ୟାନ୍ୟ ପ୍ରୟୋଗରେ ପଥ ଦୈର୍ଘ୍ୟର ଗୁରୁତ୍ୱ ଅଧିକ।ଫଟୋଏହା ଏକ ୱେଫରରେ ବହୁ ସ୍ତର (ସାଧାରଣତଃ 10 ରୁ 30) ପ୍ୟାଟର କରି ନିର୍ମିତ ହୁଏ, ଯାହା ଅନେକ ବହୁଭୁଜ ଆକୃତିରେ ଗଠିତ, ପ୍ରାୟତଃ GDSII ଫର୍ମାଟରେ ପ୍ରତିନିଧିତ୍ୱ କରାଯାଏ। ଫଟୋମାସ୍କ ନିର୍ମାତାଙ୍କୁ ଫାଇଲ ପଠାଇବା ପୂର୍ବରୁ, ଡିଜାଇନର ସଠିକତା ଯାଞ୍ଚ କରିବା ପାଇଁ PIC ସିମୁଲେଟ୍ କରିବାକୁ ସକ୍ଷମ ହେବା ଦୃଢ଼ ଭାବରେ ବାଞ୍ଛନୀୟ। ସିମୁଲେସନ୍କୁ ଅନେକ ସ୍ତରରେ ବିଭକ୍ତ କରାଯାଇଛି: ସର୍ବନିମ୍ନ ସ୍ତର ହେଉଛି ତ୍ରି-ପରିମାଣୀୟ ବିଦ୍ୟୁତ୍-ଚୁମ୍ବକୀୟ (EM) ସିମୁଲେସନ୍, ଯେଉଁଠାରେ ସିମୁଲେସନ୍ ଉପ-ତରଙ୍ଗଦୈର୍ଘ୍ୟ ସ୍ତରରେ କରାଯାଏ, ଯଦିଓ ସାମଗ୍ରୀରେ ପରମାଣୁ ମଧ୍ୟରେ ପାରସ୍ପରିକ କ୍ରିୟା ମାକ୍ରୋସ୍କୋପିକ୍ ସ୍କେଲରେ ପରିଚାଳିତ ହୁଏ। ସାଧାରଣ ପଦ୍ଧତିଗୁଡ଼ିକରେ ତ୍ରି-ପରିମାଣୀୟ ସସୀମ-ପାର୍ଥକ୍ୟ ସମୟ-ଡୋମେନ୍ (3D FDTD) ଏବଂ ଇଜେନମୋଡ୍ ବିସ୍ତାର (EME) ଅନ୍ତର୍ଭୁକ୍ତ। ଏହି ପଦ୍ଧତିଗୁଡ଼ିକ ସବୁଠାରୁ ସଠିକ, କିନ୍ତୁ ସମଗ୍ର PIC ସିମୁଲେସନ୍ ସମୟ ପାଇଁ ଅବାସ୍ତବ। ପରବର୍ତ୍ତୀ ସ୍ତର ହେଉଛି 2.5-ପରିମାଣୀୟ EM ସିମୁଲେସନ୍, ଯେପରିକି ସସୀମ-ପାର୍ଥକ୍ୟ ବିମ୍ ପ୍ରସାରଣ (FD-BPM)। ଏହି ପଦ୍ଧତିଗୁଡ଼ିକ ବହୁତ ଦ୍ରୁତ, କିନ୍ତୁ କିଛି ସଠିକତା ବଳିଦାନ କରେ ଏବଂ କେବଳ ପାରାକ୍ସିଆଲ୍ ପ୍ରସାରଣକୁ ପରିଚାଳନା କରିପାରିବ ଏବଂ ଉଦାହରଣ ସ୍ୱରୂପ, ରେଜୋନେଟରଗୁଡ଼ିକୁ ସିମୁଲେଟ୍ କରିବାକୁ ବ୍ୟବହାର କରାଯାଇପାରିବ ନାହିଁ। ପରବର୍ତ୍ତୀ ସ୍ତର ହେଉଛି 2D EM ସିମୁଲେସନ, ଯେପରିକି 2D FDTD ଏବଂ 2D BPM। ଏଗୁଡ଼ିକ ମଧ୍ୟ ଦ୍ରୁତ, କିନ୍ତୁ ସୀମିତ କାର୍ଯ୍ୟକ୍ଷମତା ଅଛି, ଯେପରିକି ଏମାନେ ଧ୍ରୁବୀକରଣ ରୋଟେଟରଗୁଡ଼ିକୁ ସିମୁଲେଟ କରିପାରିବେ ନାହିଁ। ଆହୁରି ଏକ ସ୍ତର ହେଉଛି ଟ୍ରାନ୍ସମିସନ୍ ଏବଂ/କିମ୍ବା ସ୍କାଟରିଂ ମ୍ୟାଟ୍ରିକ୍ସ ସିମୁଲେସନ। ପ୍ରତ୍ୟେକ ପ୍ରମୁଖ ଉପାଦାନକୁ ଇନପୁଟ୍ ଏବଂ ଆଉଟପୁଟ୍ ସହିତ ଏକ ଉପାଦାନରେ ହ୍ରାସ କରାଯାଇଛି, ଏବଂ ସଂଯୁକ୍ତ ୱେଭଗାଇଡ୍ ଏକ ପର୍ଯ୍ୟାୟ ସ୍ଥାନାନ୍ତର ଏବଂ ଆଟେନୁଏସନ୍ ଉପାଦାନକୁ ହ୍ରାସ କରାଯାଇଛି। ଏହି ସିମୁଲେସନଗୁଡ଼ିକ ଅତ୍ୟନ୍ତ ଦ୍ରୁତ। ଇନପୁଟ୍ ସିଗନାଲ ଦ୍ୱାରା ଟ୍ରାନ୍ସମିସନ୍ ମାଟ୍ରିକ୍ସକୁ ଗୁଣନ କରି ଆଉଟପୁଟ୍ ସିଗନାଲ ପ୍ରାପ୍ତ ହୁଏ। ବିକ୍ଷିପ୍ତ ମାଟ୍ରିକ୍ସ (ଯାହାର ଉପାଦାନଗୁଡ଼ିକୁ S-ପାରାମିଟର କୁହାଯାଏ) ଉପାଦାନର ଅନ୍ୟ ପାର୍ଶ୍ୱରେ ଇନପୁଟ୍ ଏବଂ ଆଉଟପୁଟ୍ ସିଗନାଲଗୁଡ଼ିକୁ ଖୋଜିବା ପାଇଁ ଗୋଟିଏ ପାର୍ଶ୍ୱରେ ଇନପୁଟ୍ ଏବଂ ଆଉଟପୁଟ୍ ସିଗନାଲଗୁଡ଼ିକୁ ଗୁଣନ କରେ। ମୂଳତଃ, ବିକ୍ଷିପ୍ତ ମାଟ୍ରିକ୍ସ ଉପାଦାନ ଭିତରେ ପ୍ରତିଫଳନ ଧାରଣ କରେ। ବିକ୍ଷିପ୍ତ ମାଟ୍ରିକ୍ସ ସାଧାରଣତଃ ପ୍ରତ୍ୟେକ ପରିମାଣରେ ଟ୍ରାନ୍ସମିସନ୍ ମାଟ୍ରିକ୍ସ ଅପେକ୍ଷା ଦୁଇଗୁଣ ବଡ଼। ସଂକ୍ଷେପରେ, 3D EM ରୁ ଟ୍ରାନ୍ସମିସନ୍/ସ୍କାଟରିଂ ମାଟ୍ରିକ୍ସ ସିମୁଲେସନ ପର୍ଯ୍ୟନ୍ତ, ସିମୁଲେସନର ପ୍ରତ୍ୟେକ ସ୍ତର ଗତି ଏବଂ ସଠିକତା ମଧ୍ୟରେ ଏକ ବାଣିଜ୍ୟ-ଅଫ୍ ଉପସ୍ଥାପନ କରେ, ଏବଂ ଡିଜାଇନର୍ମାନେ ଡିଜାଇନ୍ ବୈଧତା ପ୍ରକ୍ରିୟାକୁ ଅପ୍ଟିମାଇଜ୍ କରିବା ପାଇଁ ସେମାନଙ୍କର ନିର୍ଦ୍ଦିଷ୍ଟ ଆବଶ୍ୟକତା ପାଇଁ ସଠିକ୍ ସ୍ତରର ସିମୁଲେସନ ବାଛନ୍ତି।
ତଥାପି, ନିର୍ଦ୍ଦିଷ୍ଟ ଉପାଦାନଗୁଡ଼ିକର ଇଲେକ୍ଟ୍ରୋମ୍ୟାଗ୍ନେଟିକ୍ ସିମୁଲେସନ୍ ଉପରେ ନିର୍ଭର କରି ଏବଂ ସମ୍ପୂର୍ଣ୍ଣ PICକୁ ସିମୁଲେଟ୍ କରିବା ପାଇଁ ଏକ ବିଚ୍ଛିନ୍ନ/ସ୍ଥାନାନ୍ତର ମାଟ୍ରିକ୍ସ ବ୍ୟବହାର କରି ପ୍ରବାହ ପ୍ଲେଟ୍ ସମ୍ମୁଖରେ ଏକ ସମ୍ପୂର୍ଣ୍ଣ ସଠିକ୍ ଡିଜାଇନ୍ ଗ୍ୟାରେଣ୍ଟି ଦିଏ ନାହିଁ। ଉଦାହରଣ ସ୍ୱରୂପ, ଭୁଲ ଗଣନା କରାଯାଇଥିବା ପଥ ଲମ୍ବ, ଉଚ୍ଚ-କ୍ରମ ମୋଡ୍କୁ ପ୍ରଭାବଶାଳୀ ଭାବରେ ଦମନ କରିବାରେ ବିଫଳ ହେଉଥିବା ମଲ୍ଟିମୋଡ୍ ୱେଭ୍ଗାଇଡ୍, କିମ୍ବା ଦୁଇଟି ୱେଭ୍ଗାଇଡ୍ ଯାହା ପରସ୍ପରର ଅତି ନିକଟତର ହୋଇ ଅପ୍ରତ୍ୟାଶିତ ସଂଯୋଗ ସମସ୍ୟା ସୃଷ୍ଟି କରେ, ସିମୁଲେସନ୍ ସମୟରେ ଅଚିହ୍ନା ହେବାର ସମ୍ଭାବନା ରହିଛି। ତେଣୁ, ଯଦିଓ ଉନ୍ନତ ସିମୁଲେସନ୍ ଉପକରଣଗୁଡ଼ିକ ଶକ୍ତିଶାଳୀ ଡିଜାଇନ୍ ବୈଧତା କ୍ଷମତା ପ୍ରଦାନ କରନ୍ତି, ତଥାପି ଡିଜାଇନର ସଠିକତା ଏବଂ ନିର୍ଭରଯୋଗ୍ୟତା ସୁନିଶ୍ଚିତ କରିବା ଏବଂ ପ୍ରବାହ ସିଟ୍ର ବିପଦକୁ ହ୍ରାସ କରିବା ପାଇଁ ବ୍ୟବହାରିକ ଅଭିଜ୍ଞତା ଏବଂ ବୈଷୟିକ ଜ୍ଞାନ ସହିତ ଡିଜାଇନରଙ୍କ ଦ୍ୱାରା ଉଚ୍ଚ ପରିମାଣର ସତର୍କତା ଏବଂ ସତର୍କତା ଯାଞ୍ଚ ଆବଶ୍ୟକ।
ସ୍ପାର୍ସ FDTD ନାମକ ଏକ କୌଶଳ ଡିଜାଇନକୁ ବୈଧ କରିବା ପାଇଁ ଏକ ସମ୍ପୂର୍ଣ୍ଣ PIC ଡିଜାଇନରେ ସିଧାସଳଖ 3D ଏବଂ 2D FDTD ସିମୁଲେସନ କରିବାକୁ ଅନୁମତି ଦିଏ। ଯଦିଓ ଯେକୌଣସି ଇଲେକ୍ଟ୍ରୋମ୍ୟାଗ୍ନେଟିକ୍ ସିମୁଲେସନ୍ ଉପକରଣ ପାଇଁ ଏକ ବହୁତ ବଡ଼ ସ୍କେଲ୍ PIC ସିମୁଲେଟ୍ କରିବା କଷ୍ଟକର, ସ୍ପାର୍ସ FDTD ଏକ ଯଥେଷ୍ଟ ବଡ଼ ସ୍ଥାନୀୟ କ୍ଷେତ୍ର ସିମୁଲେଟ୍ କରିବାକୁ ସକ୍ଷମ। ପାରମ୍ପରିକ 3D FDTDରେ, ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ପରିମାଣଯୁକ୍ତ ଭଲ୍ୟୁମ୍ ମଧ୍ୟରେ ଇଲେକ୍ଟ୍ରୋମ୍ୟାଗ୍ନେଟିକ୍ କ୍ଷେତ୍ରର ଛଅଟି ଉପାଦାନକୁ ଆରମ୍ଭ କରି ସିମୁଲେସନ୍ ଆରମ୍ଭ ହୁଏ। ସମୟ ବଢ଼ିବା ସହିତ, ଭଲ୍ୟୁମ୍ରେ ନୂତନ କ୍ଷେତ୍ର ଉପାଦାନ ଗଣନା କରାଯାଏ, ଇତ୍ୟାଦି। ପ୍ରତ୍ୟେକ ପଦକ୍ଷେପ ପାଇଁ ବହୁତ ଗଣନା ଆବଶ୍ୟକ, ତେଣୁ ଏହା ବହୁତ ସମୟ ନେଇଥାଏ। ସ୍ପାର୍ସ 3D FDTDରେ, ଭଲ୍ୟୁମ୍ର ପ୍ରତ୍ୟେକ ବିନ୍ଦୁରେ ପ୍ରତ୍ୟେକ ପଦକ୍ଷେପରେ ଗଣନା କରିବା ପରିବର୍ତ୍ତେ, କ୍ଷେତ୍ର ଉପାଦାନଗୁଡ଼ିକର ଏକ ତାଲିକା ରଖାଯାଏ ଯାହା ତତ୍ତ୍ୱଗତ ଭାବରେ ଏକ ମନଇଚ୍ଛା ବଡ଼ ଭଲ୍ୟୁମ୍ ସହିତ ମେଳ ଖାଇପାରେ ଏବଂ କେବଳ ସେହି ଉପାଦାନଗୁଡ଼ିକ ପାଇଁ ଗଣନା କରାଯାଇପାରିବ। ପ୍ରତ୍ୟେକ ସମୟ ପଦକ୍ଷେପରେ, କ୍ଷେତ୍ର ଉପାଦାନଗୁଡ଼ିକ ସହିତ ସଂଲଗ୍ନ ବିନ୍ଦୁଗୁଡ଼ିକ ଯୋଡାଯାଏ, ଯେତେବେଳେ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଶକ୍ତି ସୀମା ତଳେ ଥିବା କ୍ଷେତ୍ର ଉପାଦାନଗୁଡ଼ିକୁ ଛାଡି ଦିଆଯାଏ। କିଛି ଗଠନ ପାଇଁ, ଏହି ଗଣନା ପାରମ୍ପରିକ 3D FDTD ଅପେକ୍ଷା ତୀବ୍ରତାର ଅନେକ କ୍ରମ ହୋଇପାରେ। ତଥାପି, ବିସ୍ତାରକାରୀ ଗଠନ ସହିତ କାର୍ଯ୍ୟ କରିବା ସମୟରେ ସ୍ପାର୍ସ FDTDS ଭଲ କାର୍ଯ୍ୟ କରେ ନାହିଁ କାରଣ ଏହି ସମୟ କ୍ଷେତ୍ର ଅତ୍ୟଧିକ ବ୍ୟାପିଥାଏ, ଯାହା ଫଳରେ ତାଲିକାଗୁଡ଼ିକ ଅତ୍ୟଧିକ ଲମ୍ବା ଏବଂ ପରିଚାଳନା କରିବା କଷ୍ଟକର ହୋଇଥାଏ। ଚିତ୍ର 1 ଏକ ଧ୍ରୁବୀକରଣ ବିମ୍ ସ୍ପ୍ଲିଟର (PBS) ପରି ଏକ 3D FDTD ସିମୁଲେସନର ଏକ ଉଦାହରଣ ସ୍କ୍ରିନସଟ୍ ଦେଖାଉଛି।
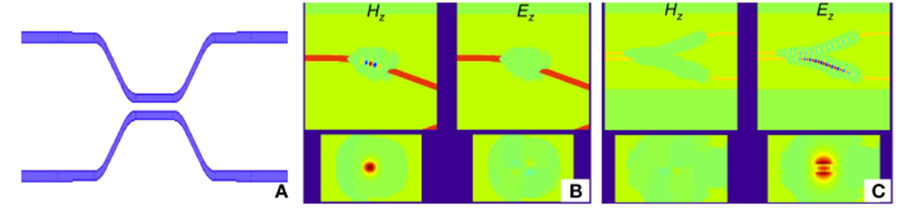
ଚିତ୍ର 1: 3D ସ୍ପାର୍ସ FDTD ରୁ ସିମୁଲେସନ ଫଳାଫଳ। (A) ହେଉଛି ସିମୁଲେଟେଡ୍ ଗଠନର ଏକ ଉପର ଦୃଶ୍ୟ, ଯାହା ଏକ ଦିଗନିର୍ଦ୍ଦେଶକ କପଲର୍। (B) କ୍ୱାସି-ଟିଇ ଉତ୍ତେଜନା ବ୍ୟବହାର କରି ଏକ ସିମୁଲେସନର ଏକ ସ୍କ୍ରିନସଟ୍ ଦେଖାଏ। ଉପରୋକ୍ତ ଦୁଇଟି ଚିତ୍ର କ୍ୱାସି-ଟିଇ ଏବଂ କ୍ୱାସି-ଟିଏମ୍ ସିଗନାଲର ଉପର ଦୃଶ୍ୟ ଦେଖାଏ, ଏବଂ ତଳେ ଥିବା ଦୁଇଟି ଚିତ୍ର ଅନୁରୂପ କ୍ରସ୍-ସେକ୍ସନାଲ୍ ଦୃଶ୍ୟ ଦେଖାଏ। (C) କ୍ୱାସି-ଟିଏମ୍ ଉତ୍ତେଜନା ବ୍ୟବହାର କରି ଏକ ସିମୁଲେସନର ଏକ ସ୍କ୍ରିନସଟ୍ ଦେଖାଏ।
ପୋଷ୍ଟ ସମୟ: ଜୁଲାଇ-୨୩-୨୦୨୪





